One friend was working on UE and wanted to create a pipeline for certain data types. For example, he would like a function that takes in a std::string and eventually wrap the string to WrappedString, or an input int to WrappedInt, etc. So the question basically is "is there a way to map types in C++".
It’s easy to do it in Python because types are treated as objects. To tackle this question, we can create a mapping from types to types, like the following example. If we were working with Rust, we can write handy macros. But in C++, macros seem to be a pain and types are not objects.
DATA_TYPE_MAPPING = {
str: WrappedString,
int: WrappedInt,
bool: WrappedBool
}
def piping(data):
# do something here ...
data_type = type(data)
try:
wrapper = DATA_TYPE_MAPPING[data_type]
except KeyError as e:
raise TypeError(f"No matched wrapper type for the type {data_type}") from e
return wrapper(data)We can of course write overloaded functions. But if the only changing things are the types and what they are mapped to, overloading seems to be too much due to duplications. For example, the following code seems quite verbose.
(The highlighted lines will be implicitly included in all the code snippets below if not specified otherwise)
#include <iostream>
template <typename S>
struct Wrapper {
S data;
};
using WrappedInt = struct Wrapper<int>;
using WrappedDouble = struct Wrapper<double>;
WrappedInt piper(int t) {
// do something, e.g.:
t = t * t;
return {t};
}
WrappedDouble piper(double t) {
// do something, e.g.:
t = t * t;
return {t};
}
int main() {
std::cout << piper(1).data << std::endl;
std::cout << piper(1.0).data << std::endl;
}We all know duplications are bad. How can we simplify that? Wait, C++ has great type checkers. Why don’t we use that!
Type checkers are wonderful things. It’s strict and precise. Unlike runtime errors that could lurk around shoot you on your feet seemingly randomly, typing errors can be checked by the compiler even before the code is compiled. Yet it’s also powerful. This post shows you how to do solve the classic N queens problem with only types! (I think in Chinese people call this "类型体操" or typing artistic gymnastics, which is describing the slick sets of actions performed by players (or types in this case), hence the name of this post).
Can we create type mappings with only types then? It turns out in this case is yes!
First, let’s create a TypeMap struct. It seems like many of the handy helpers in the <type_traits> header is defined with a struct. It looks like a plausible way to start. You can check out examples like true_type and is_same. In the code below, given any type T, say TypeMap<int>, the TypeMap<T> will contain nothing. Ok? How do we do the mapping then?
template <typename T>
struct TypeMap {};We can utilize the partial template specification to create specific mapping pairs. In the highlighted lines, TypeMap are not parametrized anymore. In the case of TypeMap<int>, the struct is defined to contain a type alias of WrappedInt, named type. Similarly, in the case of double, we create a type alias also named type for WrappedDouble. Once those are written down, whenever we mention TypeMap<int> and TypeMap<double>, C++ will use the specific versions and allows us to access the type by using the scope resolution operator ::. For example, TypeMap<int>::type will be evaluated to WrappedInt.
template <typename T>
struct TypeMap {};
template <>
struct TypeMap<int> {
using type = WrappedInt;
};
template <>
struct TypeMap<double> {
using type = WrappedDouble;
};With specific mappings defined, we can try to write a parametrized function that takes in an input of type T and returns WrappedT, where T can only be int and double in our example. Let’s call the function piper that does some processing and returns our input wrapped a specific wrapper type. You can see that the return type of piper is now typename TypeMap<S>, which is the mapping result from the type S. (typename is used because we are accessing a dependent type name)
template <typename T>
struct TypeMap {};
template <>
struct TypeMap<int> {
using type = WrapperInt;
};
template <>
struct TypeMap<double> {
using type = WrapperDouble;
};
template <typename S>
typename TypeMap<S>::type piper(S t) {
t = t * t;
return {t};
}
int main() {
std::cout << piper(1).data << std::endl;
std::cout << piper(1.0).data << std::endl;
}How exciting! We have a type mapping! C++ thinks it’s valid and it looks like it does the things we want it to do!
But, you may say, what if I write piper("a string") or pass in arguments that are not specified in the TypeMap? What would the type checker think?
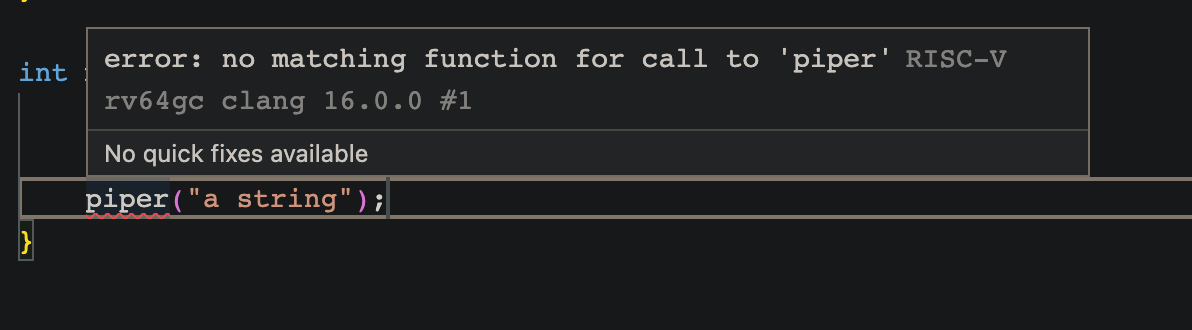
Ta-dah! Compiler knows it’s wrong! We have safe code and no copying-pasting is required anymore!
The links to the compiled version of the function-overloading and the template C++ code are here and here, respectively. You can see that no overhead is added, for we only uses types that are stripped away in compiling time.
Can you solve N queens with only types in C++ then? Maybe I’ll update on that one. But for now, I hope you enjoy this and have a good day (imitating James Hoffmann and his smile). :) Ok there we go! The executed result is here. You can also look at the code below. Thank you so much for reading. I hope you have a great day! (imitating James Hoffmann and his smile again) :)
#include <iostream>
#include <typeinfo>
#include <boost/core/demangle.hpp> // enable if you can use boost to demangle the type name
// logics
struct True {
using val = True;
};
struct False {
using val = False;
};
template <typename T>
struct Not {};
template <>
struct Not<True> {
using val = False;
};
template <>
struct Not<False> {
using val = True;
};
template <typename C, typename T, typename E>
struct If {};
template <typename T, typename E>
struct If<True, T, E> {
using val = T;
};
template <typename T, typename E>
struct If<False, T, E> {
using val = E;
};
template <typename T, typename S>
struct And {};
template <typename T>
struct And<False, T> {
using val = False;
};
template <typename T>
struct And<True, T> {
using val = T;
};
template <typename T, typename S>
struct Or {};
template <typename T>
struct Or<True, T> {
using val = True;
};
template <typename T>
struct Or<False, T> {
using val = T;
};
// numbers
struct Zero {
using val = struct Zero;
};
template <typename T>
struct Succ {
using val = struct Succ<T>;
};
template <>
struct Succ<Zero> {
using val = struct Succ<Zero>;
};
// make number
template <unsigned long long N>
struct MakeNumber {
using val = Succ<typename MakeNumber<N - 1>::val>;
};
template <>
struct MakeNumber<0> {
using val = Zero;
};
// the size of the board
using N = typename MakeNumber<6>::val;
// predecessor
template <typename T>
struct Pred {};
template <>
struct Pred<Zero> {};
template <typename T>
struct Pred<Succ<T>> {
using val = T;
};
// abs difference
template <typename T, typename S>
struct AbsDiff {
using val = typename AbsDiff<typename Pred<T>::val, typename Pred<S>::val>::val;
};
template <typename T>
struct AbsDiff<Zero, T> {
using val = T;
};
template <typename T>
struct AbsDiff<T, Zero> {
using val = T;
};
template <>
struct AbsDiff<Zero, Zero> {
using val = Zero;
};
// List
struct Nil {
using val = Nil;
};
template <typename X, typename Xs = Nil>
struct Cons {
using val = Cons<X, Xs>;
using x = X;
using xs = Xs;
};
// Equality for numbers and lists
template <typename X, typename Y, typename Xs = Nil, typename Ys = Nil>
struct Equals {};
template <typename X, typename Y, typename Xs, typename Ys>
struct Equals<Cons<X, Xs>, Cons<Y, Ys>> {
using val = typename And<
typename Equals<X, Y>::val,
typename Equals<Xs, Ys>::val
>::val;
};
template <>
struct Equals<Nil, Nil> {
using val = True;
};
template <typename Xs>
struct Equals<Nil, Xs> {
using val = False;
};
template <typename Xs>
struct Equals<Xs, Nil> {
using val = False;
};
template <>
struct Equals<Zero, Zero> {
using val = True;
};
template <typename T>
struct Equals<Zero, T> {
using val = False;
};
template <typename T>
struct Equals<T, Zero> {
using val = False;
};
template <typename T, typename S>
struct Equals<Succ<T>, Succ<S>> {
using val = typename Equals<T, S>::val;
};
// or we can do equality the easy way
// ~~but who likes the easy way?~~
// template <typename T, typename S>
// struct Equals {
// using val = False;
// };
// template <typename T>
// struct Equals<T, T> {
// using val = True;
// };
// If any in the list is true
template <typename E, typename Es = Nil>
struct AnyTrue {};
template <typename E, typename Es>
struct AnyTrue<Cons<E, Es>> {
using val = typename Or<
E,
typename AnyTrue<Es>::val
>::val;
};
template <>
struct AnyTrue<Nil> {
using val = False;
};
// Create a list of numbers from 0 to N
template <typename N, typename Xs = Nil>
struct RangeFromZero {
using xs = typename RangeFromZero<typename Pred<N>::val, Xs>::val;
using val = Cons<N, xs>;
};
template <typename Xs>
struct RangeFromZero<Zero, Xs> {
using val = Cons<Zero, Xs>;
};
// the queen
template <typename X, typename Y>
struct Queen {
using val = Queen<X, Y>;
using x = X;
using y = Y;
};
// representing a row of queen
template <typename Col, typename row, typename Cols = Nil>
struct RowOfQueens {};
template <typename Col, typename Row, typename Cols>
struct RowOfQueens<Cons<Col, Cols>, Row> {
using val = Cons<
Queen<Col, Row>,
typename RowOfQueens<Cols, Row>::val
>;
};
template <typename Row>
struct RowOfQueens<Nil, Row> {
using val = Nil;
};
// check if a queen is threatened by another queen, horizontally, vertically or diagonally
template <typename A, typename B>
struct Threatens {
using val = typename Or<
typename Or<
typename Equals<typename A::x, typename B::x>::val,
typename Equals<typename A::y, typename B::y>::val
>::val,
typename Equals<
typename AbsDiff<typename A::x, typename B::x>::val,
typename AbsDiff<typename A::y, typename B::y>::val
>::val
>::val;
};
// check if any of the queen is threatening queen Q
template <typename PlacedQueen, typename Q, typename RemainingQ = Nil>
struct ThreateningQueens {};
template <typename PlacedQueen, typename Q, typename RemainingQ>
struct ThreateningQueens<Cons<PlacedQueen, RemainingQ>, Q> {
using val = Cons<typename Threatens<PlacedQueen, Q>::val, typename ThreateningQueens<RemainingQ, Q>::val>;
};
template <typename Q>
struct ThreateningQueens<Nil, Q> {
using val = Nil;
};
// check if the queen Q is safe
template <typename PlacedQueens, typename Q>
struct Safe {
using val = typename Not<typename AnyTrue<typename ThreateningQueens<PlacedQueens, Q>::val>::val>::val;
};
// try to add more safe queens to placed queens
template <typename Candidate, typename PlacedQueens, typename RemainingC = Nil>
struct SafeQueens {};
template <typename Candidate, typename PlacedQueens, typename RemainingC>
struct SafeQueens<Cons<Candidate, RemainingC>, PlacedQueens> {
using val = typename If<
typename Safe<PlacedQueens, Candidate>::val,
Cons<Candidate, typename SafeQueens<RemainingC, PlacedQueens>::val>,
typename SafeQueens<RemainingC, PlacedQueens>::val
>::val;
};
template <typename PlacedQueens>
struct SafeQueens<Nil, PlacedQueens> {
using val = Nil;
};
// next row of queen
template <typename row, typename PlacedQueens = Nil>
struct Next {
using val = typename SafeQueens<typename RowOfQueens<typename RangeFromZero<N>::val, row>::val, PlacedQueens>::val;
};
// solve the problem
template <typename Candidates, typename row, typename PlacedQueens>
struct Solve;
// solve a row
template <typename row, typename PlacedQueens>
struct SolveNextRow {
using val = typename Solve<typename Next<Succ<row>, PlacedQueens>::val, Succ<row>, PlacedQueens>::val;
};
// solve all rows
template <typename Candidates, typename row, typename PlacedQueens>
struct Solve {
using val = typename If<
typename Equals<row, N>::val,
Cons<typename Candidates::x, PlacedQueens>,
typename If<
typename Equals<typename SolveNextRow<row, Cons<typename Candidates::x, PlacedQueens>>::val, Nil>::val,
typename Solve<typename Candidates::xs, row, PlacedQueens>::val,
typename SolveNextRow<row, Cons<typename Candidates::x, PlacedQueens>>::val
>::val
>::val;
};
template <typename row, typename PlacedQueens>
struct Solve<Nil, row, PlacedQueens> {
using val = Nil;
};
// THE SOLUTION!
using Solution = typename Solve<typename Next<Zero>::val, Zero, Nil>::val;
// debug flag
#define DEBUG false
int main() {
if (DEBUG) {
std::cout << std::endl;
std::cout << typeid(Equals<Succ<Zero>::val, Succ<Zero>>::val).name() << std::endl;
std::cout << typeid(Equals<Zero, Zero>::val).name() << std::endl;
std::cout << typeid(Equals<Succ<Zero>::val, Zero::val>::val).name() << std::endl;
std::cout << std::endl;
std::cout << typeid(AbsDiff<Succ<Zero>::val, Succ<Zero>>::val).name() << std::endl;
std::cout << typeid(AbsDiff<Zero, Zero>::val).name() << std::endl;
std::cout << (typeid(AbsDiff<Succ<Succ<Zero>>::val, Zero::val>::val).name() == typeid(Succ<Succ<Zero>>::val).name()) << std::endl;
std::cout << (typeid(AbsDiff<Succ<Succ<Zero>>::val, Succ<Zero>::val>::val).name() == typeid(Succ<Zero>::val).name()) << std::endl;
std::cout << std::endl;
std::cout << (typeid(RangeFromZero<Zero>::val).name() == typeid(Cons<Zero>::val).name()) << std::endl;
std::cout << (typeid(RangeFromZero<Succ<Succ<Succ<Zero>>>>::val).name() ==
typeid(Cons<
Succ<Succ<Succ<Zero>>>,
Cons<
Succ<Succ<Zero>>,
Cons<
Succ<Zero>,
Cons<Zero>
>
>
>::val).name()) << std::endl;
}
std::cout << std::endl;
std::cout << boost::core::demangle(typeid(Solution).name()) << std::endl; // demangled type name
// std::cout << typeid(Solution).name() << std::endl; // mangled type name
/*
* Cons<
Queen<Succ<Zero>, Succ<Succ<Succ<Succ<Succ<Succ<Zero>>>>>>>, => Queen(1, 6)
Cons<
Queen<Succ<Succ<Succ<Zero>>>, Succ<Succ<Succ<Succ<Succ<Zero>>>>>>, => Queen(3, 5)
Cons<
Queen<Succ<Succ<Succ<Succ<Succ<Zero>>>>>, Succ<Succ<Succ<Succ<Zero>>>>>, => Queen(5, 4)
Cons<
Queen<Zero, Succ<Succ<Succ<Zero>>>>, => Queen(0, 3)
Cons<
Queen<Succ<Succ<Zero>>, Succ<Succ<Zero>>>, => Queen(2, 2)
Cons<
Queen<Succ<Succ<Succ<Succ<Zero>>>>, Succ<Zero>>, => Queen(4, 1)
Cons<
Queen<Succ<Succ<Succ<Succ<Succ<Succ<Zero>>>>>>, Zero>, => Queen(6, 0)
Nil>>>>>>>
*/
return 0;
}